Skala Om en byggnadsingenjör vill göra en ritning av ett hus, kan han inte göra det i naturlig storlek. Han måste göra en förminskning av verkligheten. På samma sätt gör en kartritare naturligtvis en förminskning av det landskap han kartlägger. Bilden i ett mikroskop är däremot en förstoring av verkligheten. För att från en bild kunna veta hur långt ett mått eller ett avstånd är i verkligheten, måste man veta i vilken skala ritningen är gjord. Skalan kan uttryckas på flera olika sätt. Vanligast är följande:

1:100	Ett till hundra	Förminskning
1:10 000	Ett till tiotusen	Förminskning
100:1	Hundra till ett	Förstoring
5 000:1	Femtusen till ett	Förstoring

Förminskning eller förstoring Om ettan står först betyder det att vi har en förminskning. Bilden är då mindre än föremålet eller verkligheten. Om skalan är 1:100 är en sträcka på bilden en hundradel av motsvarande sträcka i verkligheten. Om skalan är 1:10 000 är en sträcka i verkligheten tiotusen gånger större än motsvarande sträcka på bilden. Om ettan står sist, betyder det att vi har en förstoring. Bilden är då större än föremålet eller verkligheten. Om skalan är 100:1 är en sträcka på bilden hundra gånger så stor som motsvarande sträcka i verkligheten. Om skalan är 5 000:1 är en sträcka i verkligheten bara en femtusendel av motsvarande sträcka på bilden. En användbar formel Om man dividerar ett avstånd på bilden, b med motsvarande avstånd i verkligheten, f får man skalan, s. Detta kan skrivas i en formel:

Skalan = bilden/föremålet

s = b/f

Man brukar i detta sammanhang kalla verkligheten för föremål, vare sig det gäller ett mikrochip eller hela Sverige. Därav kommer förkortningen f. Hur stort är avståndet i verkligheten? På en karta i skala 1:500 000 är avståndet mellan två orter 8 cm. Hur stort är avståndet i verkligheten? Du kan tänka så här: Varje avstånd i verkligheten är 500 000 gånger så stort som samma avstånd på kartan. Du ska alltså multiplicera 8 cm med 500 000. Sedan gäller det att hålla rätt på enheterna.

Lösning:	Avståndet i verkligheten är 500 000 · 8 cm = 4 000 000 cm =
	400 000 dm = 40 000 m = 40 km = 4 mil
Svar:	Avståndet är 4 mil

Du kan också använda formeln, även om det just här blir lite klumpigare.

Lösning:	s = b/f
	1/500 000 = 8/f
	f = 500 000 · 8
	f = 4 000 000
	4 000 000 cm = 4 mil
Svar:	Avståndet är 4 mil

Hur stort är avståndet på kartan? Avståndet mellan två orter är i verkligheten 8 km. Hur stort är avståndet på en karta i skala 1:200 000? Enklast tänker du så här: På kartan är alla avstånd en tvåhundratusendel av vad de är i verkligheten. Du ska alltså dividera 8 km med 200 000. För att divisionen ska bli lättare, gör du om 8 km till cm.

Lösning:	8 km = 8 000 m = 800 000 cm
	Avstånd på kartan: 8 km/200 000 = 800 000 cm/200 000 = 4 cm
Svar:	På kartan blir avståndet 4 cm

Även här kan du använda formeln.

Lösning:	s = b/f
	1/200 000 = b/800 000
	800 000/200 000 = b
	4 = b
Svar:	På kartan blir avståndet 4 cm

Vilken skala har man använt? På en karta är avståndet mellan två orter 4 cm. I verkligheten är avståndet mellan orterna 12 km. I vilken skala är kartan ritad? När man frågar efter skalan, är formeln alldeles utmärkt att använda. Du måste bara tänka på att få samma enhet både i täljaren och nämnaren. I det här fallet är det klart enklast att göra om 12 km till cm.

Lösning:	12 km = 12 000 m = 1 200 000 cm
	s = b/f
	s = 4/1 200 000
	s = 1/300 000 (förkortat med 4)
Svar:	Kartan är ritad i skala 1:300 000

Ytterligare några exempel Herr L betraktar ett 0,03 mm stort föremål i ett mikroskop som förstorar 500 gånger. Hur stort ser föremålet ut att vara i mikroskopet?

Lösning:	Mikroskopbilden är 500 · 0,03 mm = 15 mm
Svar:	Det ser ut att vara 15 mm

På en byggnadsritning i skala 1:100 är en vägg 4,5 cm lång. Hur lång är väggen i verkligheten?

Lösning:	Väggens längd är 100 · 4,5 cm = 450 cm
Svar:	Väggen är 4,5 m lång

Ett mikroskop förstorar 200 gånger. I mikroskopet ser ett flimmerhår ut att vara 3 mm tjockt. Hur tjockt är flimmerhåret i verkligheten?

Lösning:	Den verkliga tjockleken: 3 mm/200 = 0,015 mm
Svar:	Flimmerhåret är 0,015 mm tjockt

Ett hårstrå är i verkligheten 0,04 mm tjockt. I ett mikroskop ser det ut att vara 2 mm tjockt. Hur många gånger förstorar mikroskopet?

Lösning:	s = b/f
	s = 2 mm/0,04 mm = 200 mm/4 mm = 50
Svar:	Mikroskopet förstorar 50 gånger

I exemplet ovan kan man också säga att skalan är 50:1. Ett lite mer komplicerat problem På en karta är avståndet mellan två orter 5 cm. Avståndet mellan dessa orter är i verkligheten 20 km. Avståndet mellan två andra orter på samma karta är 7,8 cm. Hur långt är avståndet mellan dessa bägge orter i verkligheten? Här måste du göra två uträkningar. Först räknar du ut skalan med hjälp av de första orterna. Sedan använder du den skalan för att beräkna avståndet mellan de bägge andra orterna.

Lösning:	s = b/f
	s = 5 cm/20 km = 5 cm/2 000 000 cm = 1/400 000
	Det andra avståndet i verkligheten:
	400 000 · 7,8 cm = 3 120 000 cm = 31,2 km
Svar:	Avståndet är 31,2 km

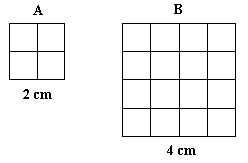
Avbildningar Ovan är två kvadrater A och B ritade. Kvadraten A har sidan 2 cm och kvadraten B har sidan 4 cm. Om du betraktar A som föremål och B som bild, blir skalan 2:1, alltså en förstoring. Uppställning: s = b/f = 4 cm/2 cm = 2 Om du däremot betraktar B som föremål och A som bild blir skalan 1:2, vilket betyder en förminskning. Uppställning: s = b/f = 2 cm/4 cm = 1/2 Det vi hittills benämnt som skala är egentligen längdskalan. När det gäller våra två kvadrater ovan talar den om att alla sträckor hos B är dubbelt så långa som motsvarande sträckor hos A. Det gör att du vet att till exempel diagonalen hos B är dubbelt så lång som diagonalen hos A, utan att du behöver räkna ut dessa sträckor. Areaskalan Här har kvadraterna sidorna 2 respektive 6 cm. Om den lilla kvadraten betraktas som föremål och den stora som bild blir längdskalan 3:1. Om du däremot jämför de bägge kvadraternas areor, finner du att den lilla kvadraten har arean 4 cm2 och den stora kvadraten har arean 36 cm2. För att beräkna areaskalan ska du dividera bildens area med föremålets area. Om den lilla kvadraten är föremål och den stora kvadraten bild blir areaskalan: Areaskalan = 36 cm2/4 cm2 = 9 Det betyder att areaskalan är 9:1. Areaskalan skiljer sig alltså från längdskalan. Om man tar längdskalan gånger sig självt, får man areaskalan. Man kan också uttrycka det så här: Areaskalan = längdskalan i kvadrat Eller så här: Areaskalan = Längdskalan2 Om längdskalan är 3:1 så blir areaskalan 3 · 3 = 9. Det vill säga 32 = 9 eller 9:1. Om längdskalan är 5:1 så blir areaskalan 5 · 5 = 25. Det vill säga 52 = 25 eller 25:1 På en byggnadsritning i skala 1:100 finns ett rum med arean 20 cm2. Hur stor är rummets area i verkligheten? Eftersom alla längdmått i verkligheten är 100 gånger så långa som på ritningen, blir alla areor 100 · 100 = 10 000 gånger så stora i verkligheten som på ritningen.

Lösning:	Areaskalan = Längdskalan2
	Areaskalan = 1002 = 100 · 100 = 10 000
	10 000 · 20 cm2 = 200 000 cm2 = 20 m2
Svar:	Rummets area är 20 m2

Lösning:	Längd i verkligheten: 200 · 3 cm = 600 cm = 6 m
	Bredd i verkligheten: 200 · 2 cm = 400 cm = 4 m
	Arean: längd · bredd = 6 m · 4 m = 24 m2
Svar:	Rummets area är 24 m2

Eller

Lösning:	Areaskalan = Längdskalan2 = 200 · 200 = 40 000
	Rummets area på ritningen: 3 cm · 2 cm = 6 cm2
	Rummets verkliga area: 40 000 · 6 cm2 = 240 000 cm2 = 24 m2
Svar:	Rummets area är 24 m2